Robust Control Design and Analysis

Funding: NASA, AFOSR

Analysis of Convex Optimization Algorithms using IQCs: Large-scale optimization has become a central topic in big data science. First-order black-box optimization methods have been widely used in related machine learning problems, since the oracle complexity of these methods can be independent of the parameter dimension. In this project, we formulate linear matrix inequality (LMI) conditions to analyze the linear convergence rates of various deterministic and stochastic optimization methods. All the resultant LMI conditions are derived using integral quadratic constraints (IQCs) and dissipation inequalities. This approach provides a unified procedure to automate analysis for different optimization methods.
Graduate Student : Bin Hu (Publications)

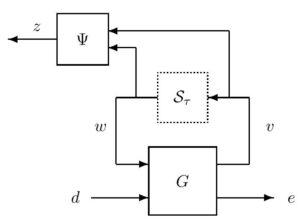
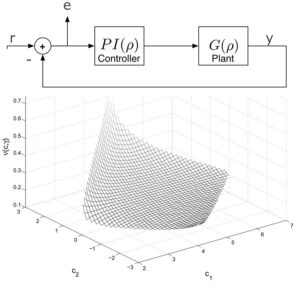
Robustness Analysis for Linear Parameter Varying Systems: This research focuses on developing tools and methods for robustness analysis of linear parameter varying (LPV) systems with respect to nonlinearities and/or uncertainties. LPV systems are a class of linear systems where the state matrices depend on (measurable) time-varying parameters. The analysis assumes the input/output behavior of the nonlinear/uncertain blocks is described by an integral quadratic constraint (IQC). Dissipation inequality conditions have been developed to bound the worst-case performance of the uncertain LPV system. These tools can be used to analyze the performance of gain-scheduled flight controllers. Future work will consider the synthesis of robust controllers for uncertain LPV systems.
Postdoctoral Researcher: Harald Pfifer (Publications)

Lower Bounds for the Gain of an LPV System: Determining the induced L2 norm of a linear, parameter-varying (LPV) system is an integral part of the analysis and robust control design procedures. In general, this norm cannot be determined explicitly. Most prior work has focused on efficiently computing upper bounds for the induced L2 gain. This work focuses on developing complementary algorithms to compute lower bounds for the induced L2 norm. The proposed lower bound algorithm has two benefits. First, the lower bound complements standard upper bound techniques. Specifically, a small gap between the bounds indicates that further computation, e.g. upper bounds with more complex Lyapunov functions, is unnecessary. Second, the lower bound algorithm returns a “bad” parameter trajectory for the LPV system that can be further analyzed to provide insight into the system performance.
Postdoctoral Researcher: Tamas Peni (Publications)